GC调优常用工具基础工具和Arthas
本文共 6622 字,大约阅读时间需要 22 分钟。
JDK提供的工具
在 linux 中,一般自带了 OpenJdk,一般情况下 JPS 等命令不能用,要么选择去安装 JPS 等插件,要么把 OpenJdk 卸载,去重新安装 Oracle 的 JDK,推荐重新安装。
在 windows 上,就是这些 exe。
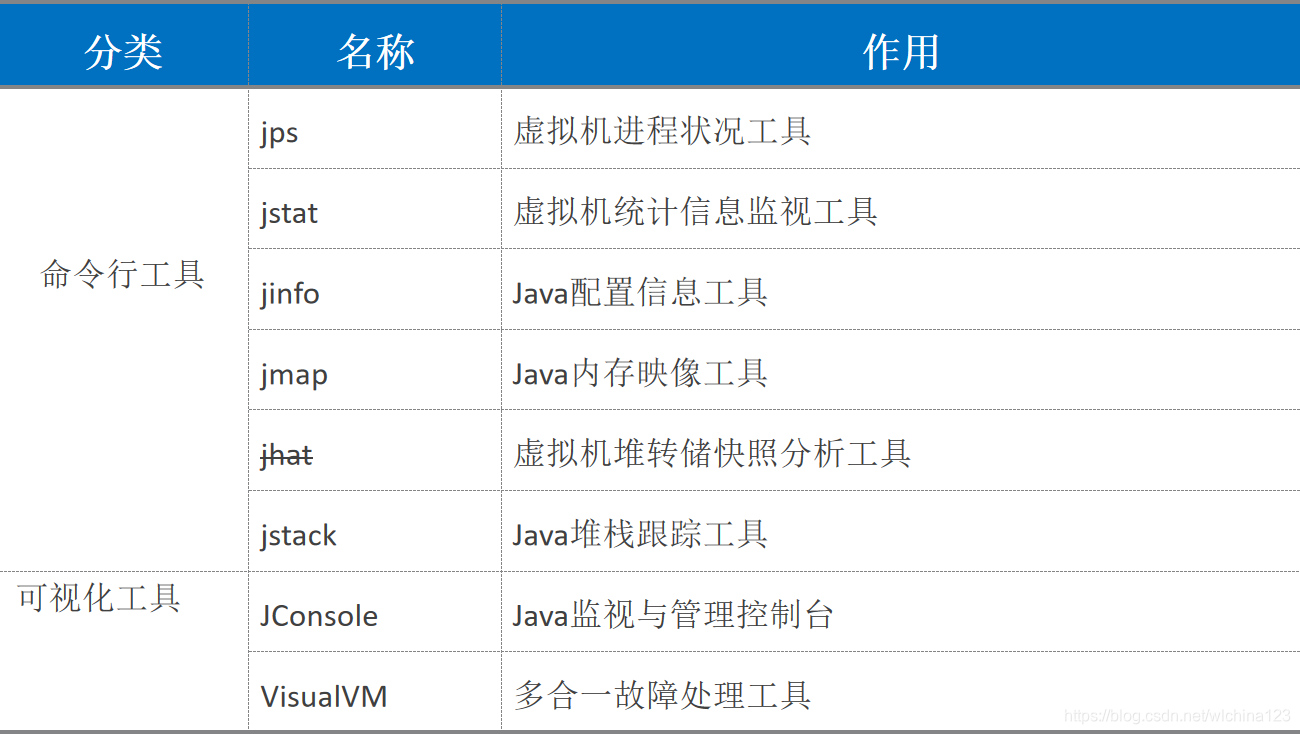
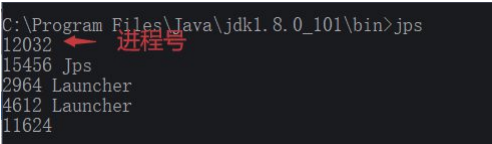 常用参数
常用参数 - -q :仅仅显示进程,
- -m:输出主函数传入的参数. 下的 hello 就是在执行程序时从命令行输入的参数
- -l: 输出应用程序主类完整 package 名称或 jar 完整名称.
- -v: 列出 jvm 参数, -Xms20m -Xmx50m 是启动程序指定的 jvm 参数
jstat
是用于监视虚拟机各种运行状态信息的命令行工具。 它可以显示本地或者远程虚拟机进程中的类装载、内存、垃圾收集、JIT 编译等运行数据,在没有 GUI 图形界面,只提供了纯文本控制台环境的服务器上,它将是运行期定位虚拟机性能问题的首选工具。 常用参数- -class (类加载器)
- -compiler (JIT)
- -gc (GC 堆状态)
- -gccapacity (各区大小)
- -gccause (最近一次 GC 统计和原因)
- -gcnew (新区统计)
- -gcnewcapacity (新区大小)
- -gcold (老区统计)
- -gcoldcapacity (老区大小)
- -gcpermcapacity (永久区大小)
- -gcutil (GC 统计汇总)
- -printcompilation (HotSpot 编译统计)
统计class类加载器:jstat -class 19064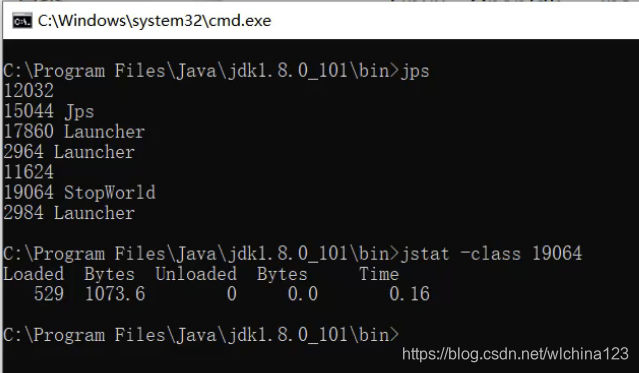
 假设需要每 1000 毫秒查询一次进程 13616 垃圾收集状况,一共查询 10 次,那命令应当是: jstat-gc 19064 1000 10
假设需要每 1000 毫秒查询一次进程 13616 垃圾收集状况,一共查询 10 次,那命令应当是: jstat-gc 19064 1000 10 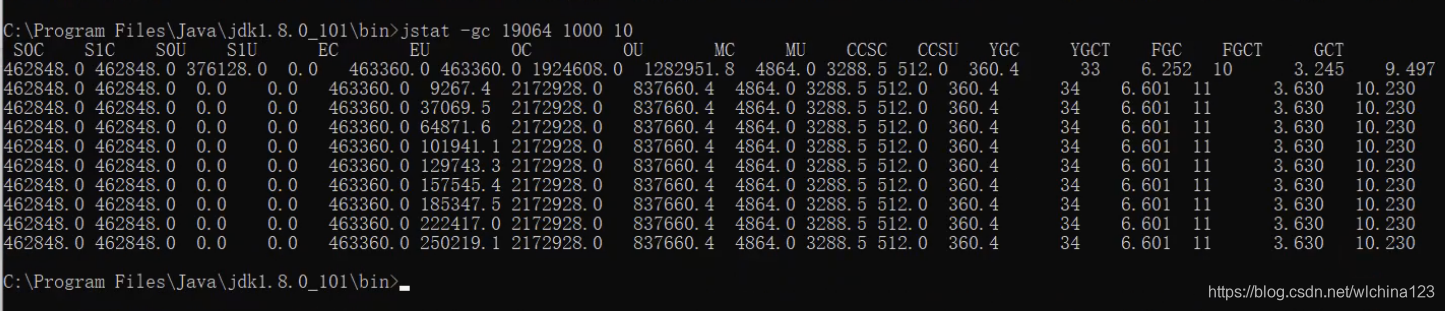 S0C:第一个幸存区(From 区)的大小 S1C:第二个幸存区(To 区)的大小 S0U:第一个幸存区的使用大小 S1U:第二个幸存区的使用大小 EC:伊甸园(Eden)区的大小 EU:伊甸园(Eden)区的使用大小 OC:老年代大小 OU:老年代使用大小 MC:方法区大小 MU:方法区使用大小 CCSC:压缩类空间大小 CCSU:压缩类空间使用大小 YGC:年轻代垃圾回收次数 YGCT:年轻代垃圾回收消耗时间 FGC:老年代垃圾回收次数 FGCT:老年代垃圾回收消耗时间 GCT:垃圾回收消耗总时间
S0C:第一个幸存区(From 区)的大小 S1C:第二个幸存区(To 区)的大小 S0U:第一个幸存区的使用大小 S1U:第二个幸存区的使用大小 EC:伊甸园(Eden)区的大小 EU:伊甸园(Eden)区的使用大小 OC:老年代大小 OU:老年代使用大小 MC:方法区大小 MU:方法区使用大小 CCSC:压缩类空间大小 CCSU:压缩类空间使用大小 YGC:年轻代垃圾回收次数 YGCT:年轻代垃圾回收消耗时间 FGC:老年代垃圾回收次数 FGCT:老年代垃圾回收消耗时间 GCT:垃圾回收消耗总时间 jinfo
查看和修改虚拟机的参数 jinfo –sysprops 可以查看由 System.getProperties()取得的参数 jinfo –flag 未被显式指定的参数的系统默认值 jinfo –flags(注意 s)显示虚拟机的参数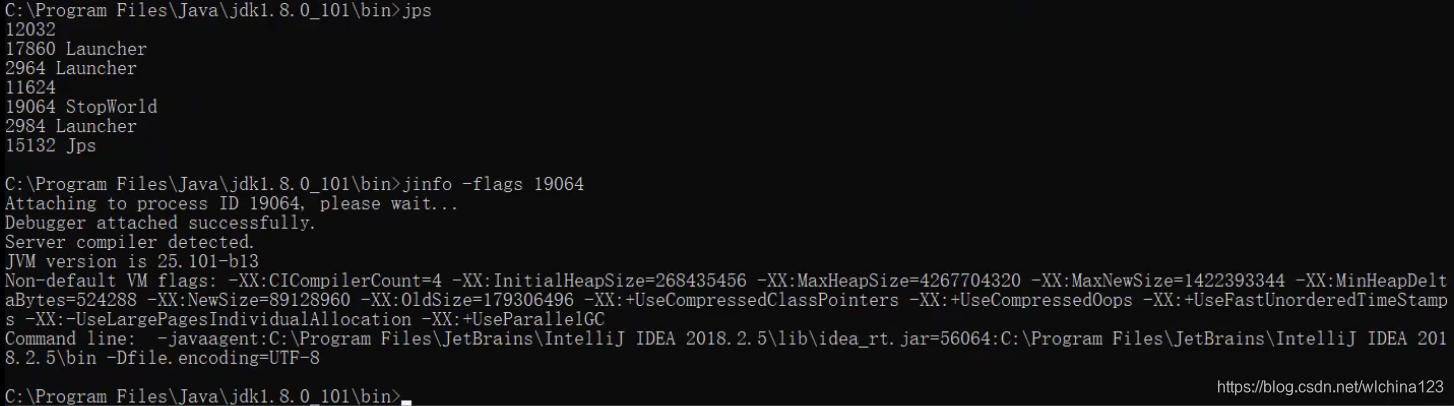
VM参数分类
:https://docs.oracle.com/javase/8/docs/technotes/tools/unix/java.html 1、标准:-开头,所有的HotSpot都支持 保证 Java 虚拟机(JVM)的所有实现都支持标准选项。它们用于执行常见操作,例如检查 JRE 版本,设置类路径,启用详细输出等 2、非标准:-X开头,特定版本HotSpot支持特定命令 非标准选项是特定于 Java HotSpot 虚拟机的通用选项,因此不能保证所有 JVM 实现都支持它们,并且它们可能会发生变化。这些选项以开头-X。 -Xms30m -Xmx30m -Xss1m
2、非标准:-X开头,特定版本HotSpot支持特定命令 非标准选项是特定于 Java HotSpot 虚拟机的通用选项,因此不能保证所有 JVM 实现都支持它们,并且它们可能会发生变化。这些选项以开头-X。 -Xms30m -Xmx30m -Xss1m  3、高级选项:以-XX开头。 这些是开发人员选项,用于调整 Java HotSpot 虚拟机操作的特定区域,这些区域通常具有特定的系统要求,并且可能需要对系统配置参数的特权访问。也 不能保证所有 JVM 实现都支持它们,并且它们可能会发生变化。
3、高级选项:以-XX开头。 这些是开发人员选项,用于调整 Java HotSpot 虚拟机操作的特定区域,这些区域通常具有特定的系统要求,并且可能需要对系统配置参数的特权访问。也 不能保证所有 JVM 实现都支持它们,并且它们可能会发生变化。  在 windows 上可以通过以下 java -XX:+PrintFlagsFinal –version 查询所有-XX 的
在 windows 上可以通过以下 java -XX:+PrintFlagsFinal –version 查询所有-XX 的 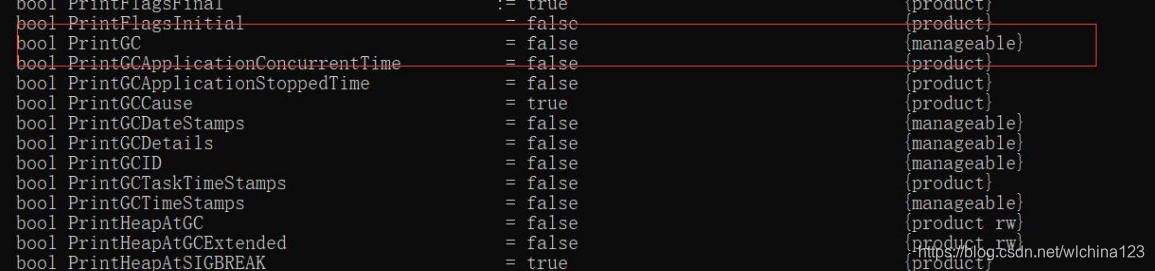 注意:manageable 的参数,代表可以运行时修改。 演示例子如下: 首先我们得知 PrintGC 这个 XX 参数是可以运行时修改的。 jinfo –flag -[参数] pid 可以修改参数 Thread.getAllStackTraces(); 案例:StopWorld 类 1.程序运行时没有打印 GC
注意:manageable 的参数,代表可以运行时修改。 演示例子如下: 首先我们得知 PrintGC 这个 XX 参数是可以运行时修改的。 jinfo –flag -[参数] pid 可以修改参数 Thread.getAllStackTraces(); 案例:StopWorld 类 1.程序运行时没有打印 GC 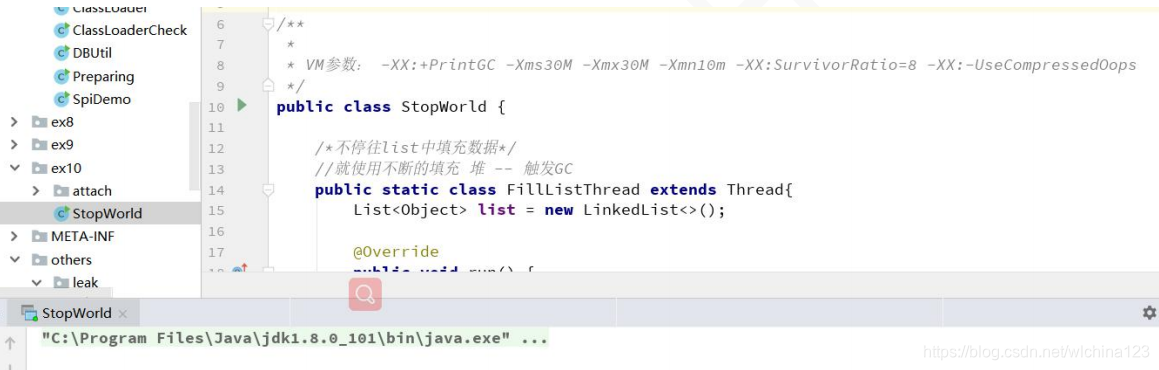 2.通过 jinfo 查看参数,打印 GC 详情
2.通过 jinfo 查看参数,打印 GC 详情 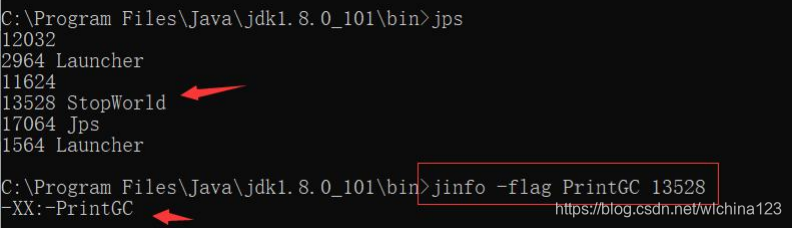 3.通过 jinfo 修改参数,打印 GC 详情
3.通过 jinfo 修改参数,打印 GC 详情 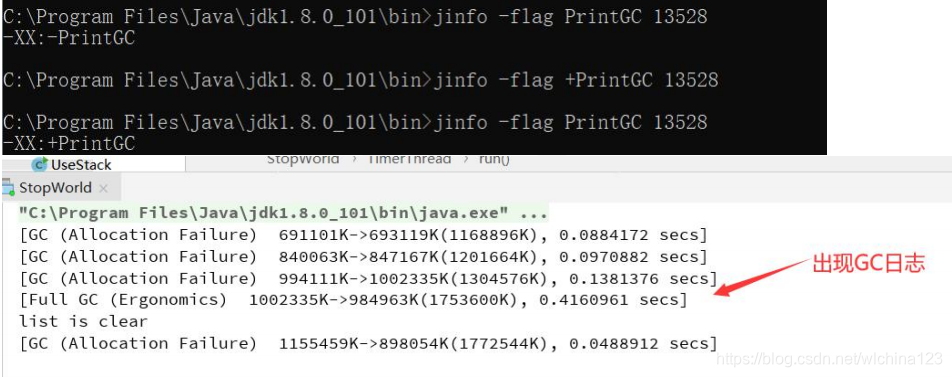
总结:通过 jinfo 命令,我可以在生产上临时打开一下 GC 日志或者进行一些数据的配置。(不需要重启应用条件下),也是我们去排查问题的一个关键命令。
jmap 用于生成堆转储快照(一般称为 heapdump 或 dump 文件)。jmap 的作用并不仅仅是为了获取 dump 文件,它还可以查询 finalize 执行队列、Java 堆和永 久代的详细信息,如空间使用率、当前用的是哪种收集器等。和 jinfo 命令一样,jmap 有不少功能在 Windows 平台下都是受限的,除了生成 dump 文件的 -dump 选项和用于查看每个类的实例、空间占用统计的-histo 选项在所有操作系统都提供之外,其余选项都只能在 Linux/Solaris 下使用。 -heap 打印 heap 的概要信息 jmap –heap 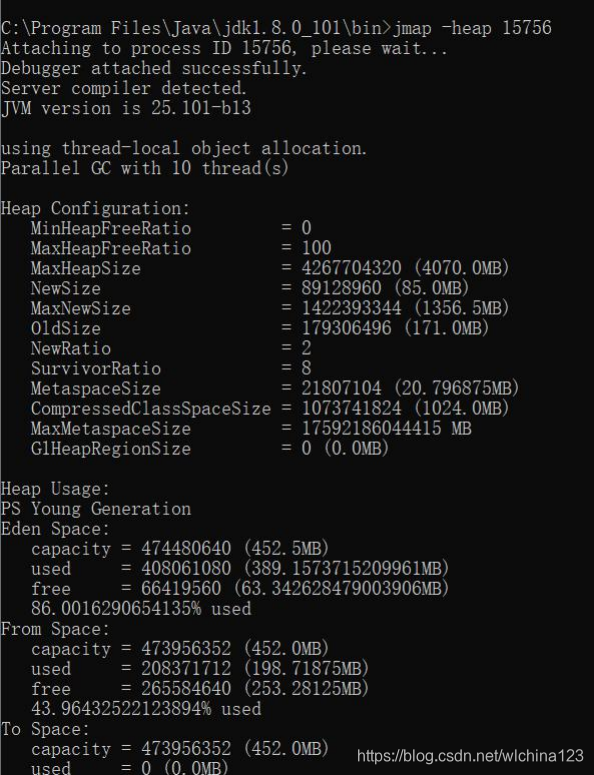 Heap Configuration: ##堆配置情况,也就是 JVM 参数配置的结果[平常说的 tomcat 配置 JVM 参数,就是在配置这些] MinHeapFreeRatio = 40 ##最小堆使用比例 MaxHeapFreeRatio = 70 ##最大堆可用比例 MaxHeapSize = 2147483648 (2048.0MB) ##最大堆空间大小 NewSize = 268435456 (256.0MB) ##新生代分配大小 MaxNewSize = 268435456 (256.0MB) ##最大可新生代分配大小 OldSize = 5439488 (5.1875MB) ##老年代大小 NewRatio = 2 ##新生代比例 SurvivorRatio = 8 ##新生代与 suvivor 的比例 PermSize = 134217728 (128.0MB) ##perm 区 永久代大小 MaxPermSize = 134217728 (128.0MB) ##最大可分配 perm 区 也就是永久代大小 Heap Usage: ##堆使用情况【堆内存实际的使用情况】 New Generation (Eden + 1 Survivor Space): ##新生代(伊甸区 Eden 区 + 幸存区 survior(1+2)空间) capacity = 241631232 (230.4375MB) ##伊甸区容量 used = 77776272 (74.17323303222656MB) ##已经使用大小 free = 163854960 (156.26426696777344MB) ##剩余容量 32.188004570534986% used ##使用比例 Eden Space: ##伊甸区 capacity = 214827008 (204.875MB) ##伊甸区容量 used = 74442288 (70.99369812011719MB) ##伊甸区使用 free = 140384720 (133.8813018798828MB) ##伊甸区当前剩余容量 34.65220164496263% used ##伊甸区使用情况 From Space: ##survior1 区 capacity = 26804224 (25.5625MB) ##survior1 区容量 used = 3333984 (3.179534912109375MB) ##surviror1 区已使用情况 free = 23470240 (22.382965087890625MB) ##surviror1 区剩余容量 12.43827838477995% used ##survior1 区使用比例 To Space: ##survior2 区 capacity = 26804224 (25.5625MB) ##survior2 区容量 used = 0 (0.0MB) ##survior2 区已使用情况 free = 26804224 (25.5625MB) ##survior2 区剩余容量 0.0% used ## survior2 区使用比例 PS Old Generation: ##老年代使用情况 capacity = 1879048192 (1792.0MB) ##老年代容量 used = 30847928 (29.41887664794922MB) ##老年代已使用容量 free = 1848200264 (1762.5811233520508MB) ##老年代剩余容量 1.6416783843721663% used ##老年代使用比例
Heap Configuration: ##堆配置情况,也就是 JVM 参数配置的结果[平常说的 tomcat 配置 JVM 参数,就是在配置这些] MinHeapFreeRatio = 40 ##最小堆使用比例 MaxHeapFreeRatio = 70 ##最大堆可用比例 MaxHeapSize = 2147483648 (2048.0MB) ##最大堆空间大小 NewSize = 268435456 (256.0MB) ##新生代分配大小 MaxNewSize = 268435456 (256.0MB) ##最大可新生代分配大小 OldSize = 5439488 (5.1875MB) ##老年代大小 NewRatio = 2 ##新生代比例 SurvivorRatio = 8 ##新生代与 suvivor 的比例 PermSize = 134217728 (128.0MB) ##perm 区 永久代大小 MaxPermSize = 134217728 (128.0MB) ##最大可分配 perm 区 也就是永久代大小 Heap Usage: ##堆使用情况【堆内存实际的使用情况】 New Generation (Eden + 1 Survivor Space): ##新生代(伊甸区 Eden 区 + 幸存区 survior(1+2)空间) capacity = 241631232 (230.4375MB) ##伊甸区容量 used = 77776272 (74.17323303222656MB) ##已经使用大小 free = 163854960 (156.26426696777344MB) ##剩余容量 32.188004570534986% used ##使用比例 Eden Space: ##伊甸区 capacity = 214827008 (204.875MB) ##伊甸区容量 used = 74442288 (70.99369812011719MB) ##伊甸区使用 free = 140384720 (133.8813018798828MB) ##伊甸区当前剩余容量 34.65220164496263% used ##伊甸区使用情况 From Space: ##survior1 区 capacity = 26804224 (25.5625MB) ##survior1 区容量 used = 3333984 (3.179534912109375MB) ##surviror1 区已使用情况 free = 23470240 (22.382965087890625MB) ##surviror1 区剩余容量 12.43827838477995% used ##survior1 区使用比例 To Space: ##survior2 区 capacity = 26804224 (25.5625MB) ##survior2 区容量 used = 0 (0.0MB) ##survior2 区已使用情况 free = 26804224 (25.5625MB) ##survior2 区剩余容量 0.0% used ## survior2 区使用比例 PS Old Generation: ##老年代使用情况 capacity = 1879048192 (1792.0MB) ##老年代容量 used = 30847928 (29.41887664794922MB) ##老年代已使用容量 free = 1848200264 (1762.5811233520508MB) ##老年代剩余容量 1.6416783843721663% used ##老年代使用比例
-histo 打印每个 class 的实例数目,内存占用,类全名信息.
jmap –histo jmap –histo:live 如果 live 子参数加上后,只统计活的对象数量.jmap -histo 19064
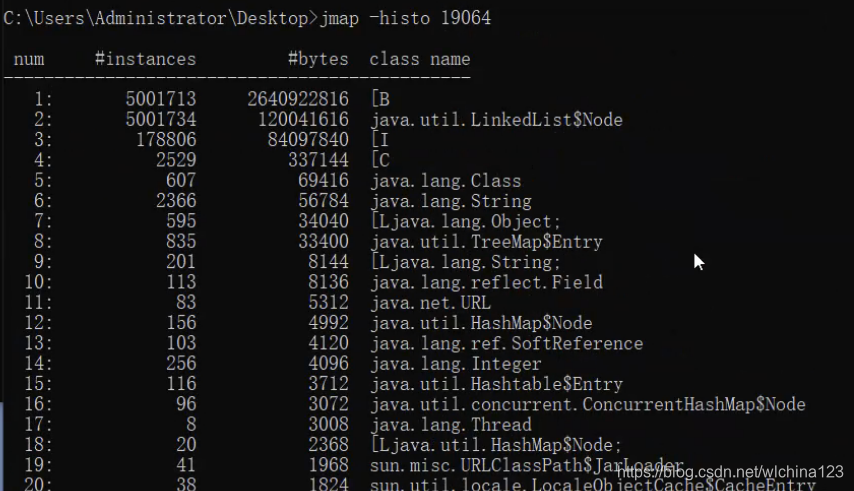 但是这样显示太多了,一般在linux上会这么操作 jmap -histo 1196 | head -20 (这样只会显示排名前20的数据)
但是这样显示太多了,一般在linux上会这么操作 jmap -histo 1196 | head -20 (这样只会显示排名前20的数据) -dump 生成的堆转储快照(比较重要)
jmap -dump:live,format=b,file=heap.bin Sun JDK 提供 jhat(JVM Heap Analysis Tool)命令与 jmap 搭配使用,来分析 jmap 生成的堆转储快照。 jstack 用于生成虚拟机当前时刻的线程快照。 一般来说 jstack 主要是用来排查是否有死锁的情况. 线程快照就是当前虚拟机内每一条线程正在执行的方法堆栈的集合,生成线程快照的主 要目的是定位线程出现长时间停顿的原因,如线程间死锁、死循环、请求外部资源导致的长时间等待等都是导致线程长时间停顿的常见原因。 在代码中可以用 java.lang.Thread 类的 getAllStackTraces()方法用于获取虚拟机中所有线程的 StackTraceElement 对象。使用这个方法可以通过简单的几行 代码就完成 jstack 的大部分功能,在实际项目中不妨调用这个方法做个管理员页面,可以随时使用浏览器来查看线程堆栈。
jstack 用于生成虚拟机当前时刻的线程快照。 一般来说 jstack 主要是用来排查是否有死锁的情况. 线程快照就是当前虚拟机内每一条线程正在执行的方法堆栈的集合,生成线程快照的主 要目的是定位线程出现长时间停顿的原因,如线程间死锁、死循环、请求外部资源导致的长时间等待等都是导致线程长时间停顿的常见原因。 在代码中可以用 java.lang.Thread 类的 getAllStackTraces()方法用于获取虚拟机中所有线程的 StackTraceElement 对象。使用这个方法可以通过简单的几行 代码就完成 jstack 的大部分功能,在实际项目中不妨调用这个方法做个管理员页面,可以随时使用浏览器来查看线程堆栈。 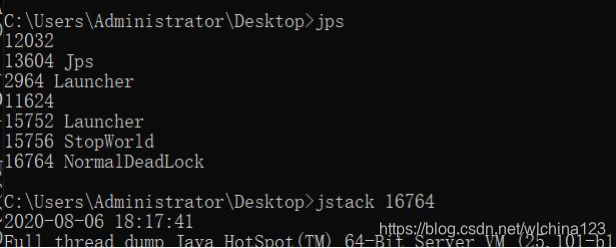
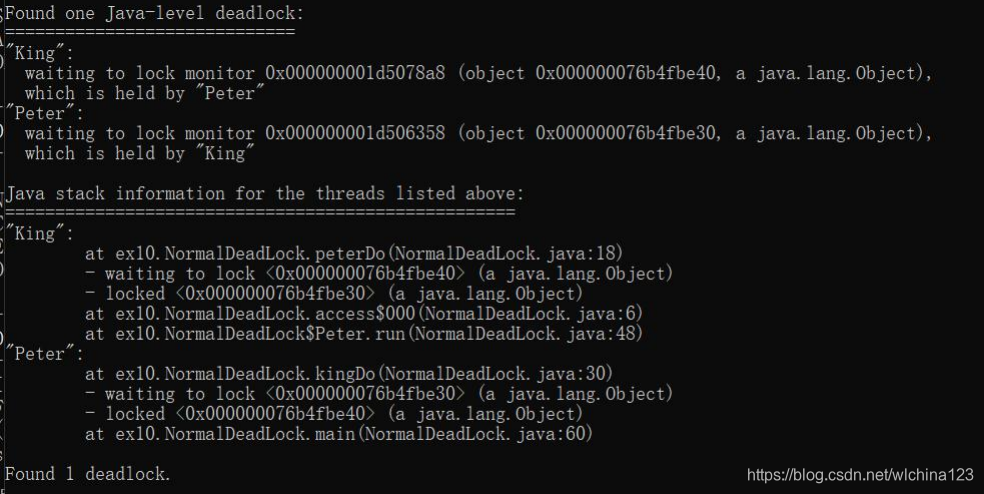
命令工具总结
生产服务器推荐开启
-XX:-HeapDumpOnOutOfMemoryError 默认关闭,建议开启,在 java.lang.OutOfMemoryError 异常出现时,输出一个 dump 文件,记录当时的堆内存快照。 -XX:HeapDumpPath=./java_pid.hprof 用来设置堆内存快照的存储文件路径,默认是 java 进程启动位置。调优之前开启、调优之后关闭
-XX:+PrintGC 调试跟踪之打印简单的 GC 信息参数: -XX:+PrintGCDetails, +XX:+PrintGCTimeStamps 打印详细的 GC 信息 -Xlogger:logpath 设置 gc 的日志路径,如: -Xlogger:log/gc.log, 将 gc.log 的路径设置到当前目录的 log 目录下. 应用场景:将 gc 的日志独立写入日志文件,将 GC 日志与系统业务日志进行了分离,方便开发人员进行追踪分析。考虑使用
-XX:+PrintHeapAtGC, 打印堆信息 参数设置: -XX:+PrintHeapAtGC 应用场景: 获取 Heap 在每次垃圾回收前后的使用状况 -XX:+TraceClassLoading 参数方法: -XX:+TraceClassLoading 应用场景:在系统控制台信息中看到 class 加载的过程和具体的 class 信息,可用以分析类的加载顺序以及是否可进行精简操作。 -XX:+DisableExplicitGC 禁止在运行期显式地调用 System.gc()可视化工具
Jconsole
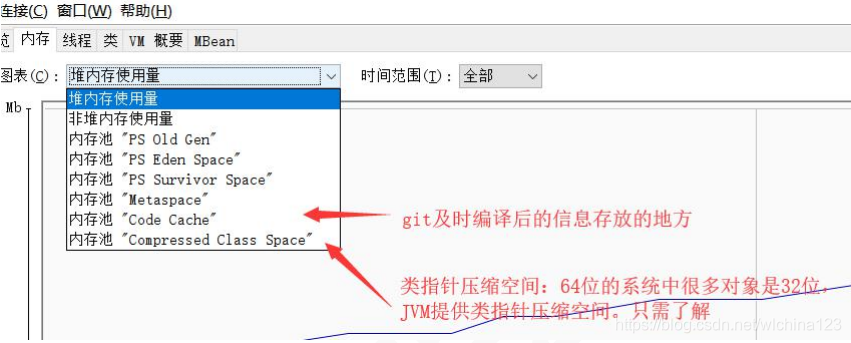
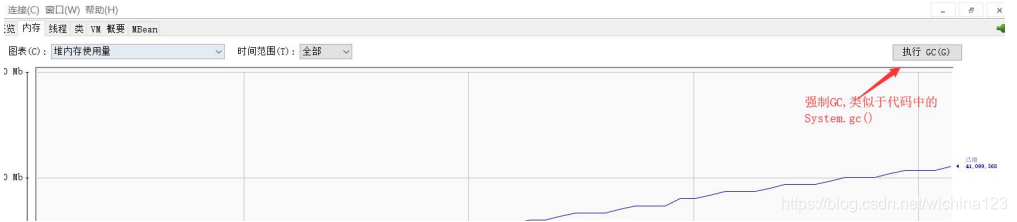
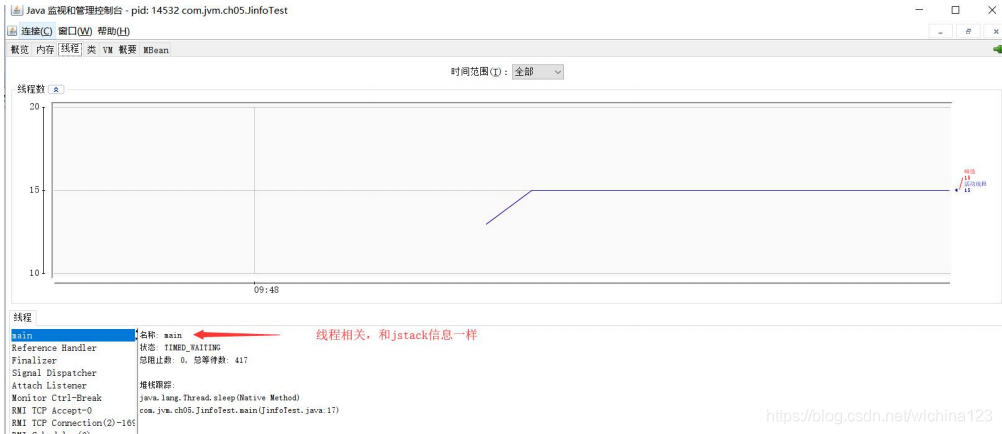
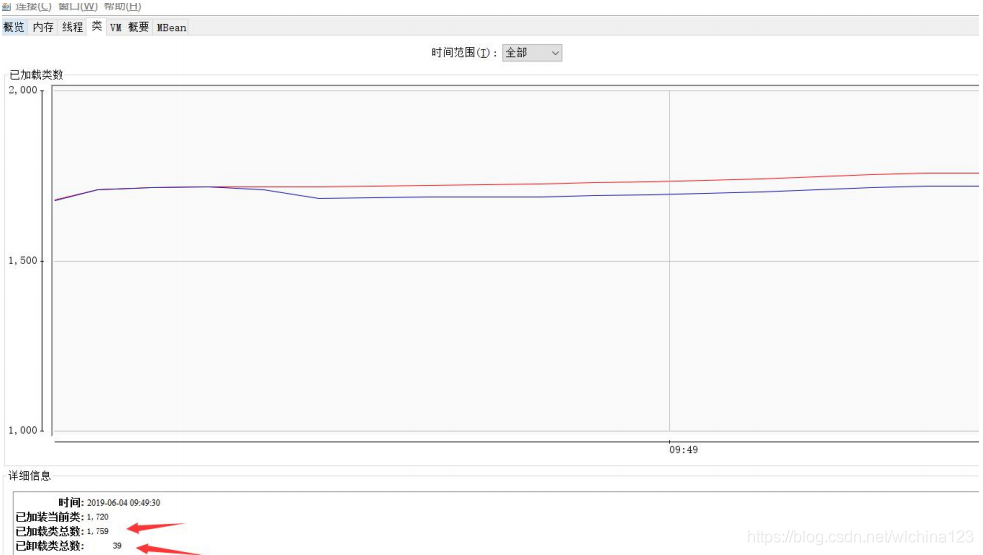
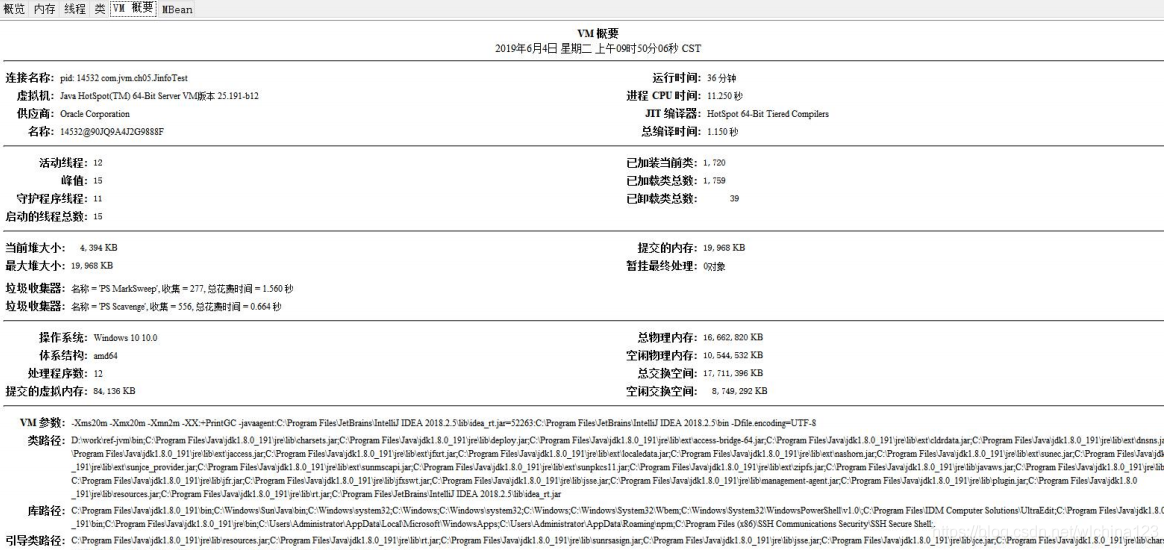 visualvm https://visualvm.github.io 但是注意版本问题,不同的 JDK 所带的 visualvm 是不一样的,下载插件时需要下对应的版本。 一般来说,这个工具是本机调试用,一般生产上来说,你一般是用不了的(除非启用远程连接)
visualvm https://visualvm.github.io 但是注意版本问题,不同的 JDK 所带的 visualvm 是不一样的,下载插件时需要下对应的版本。 一般来说,这个工具是本机调试用,一般生产上来说,你一般是用不了的(除非启用远程连接) 
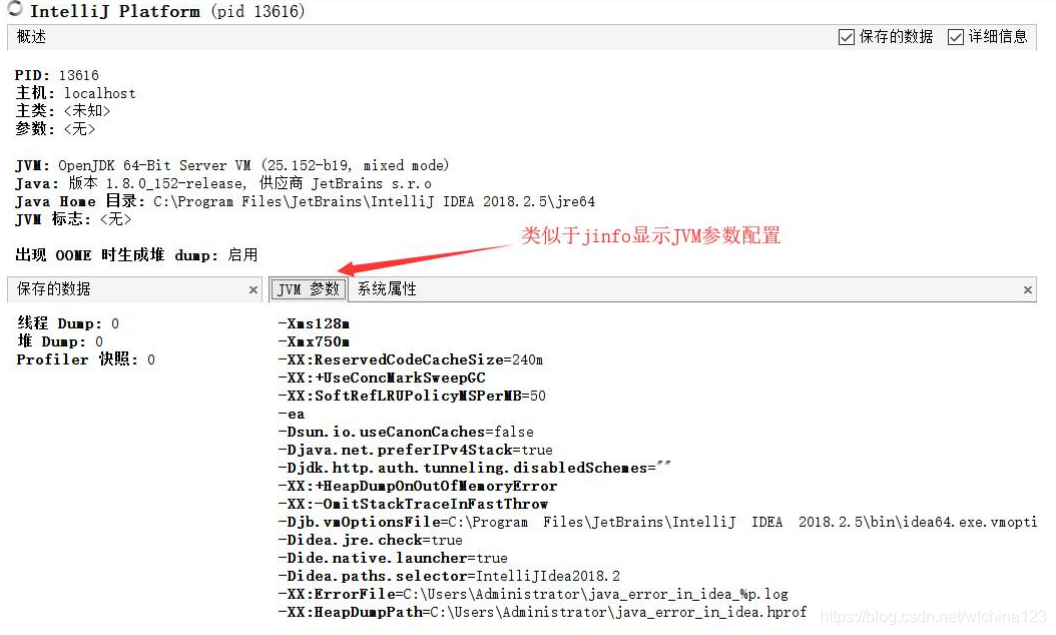
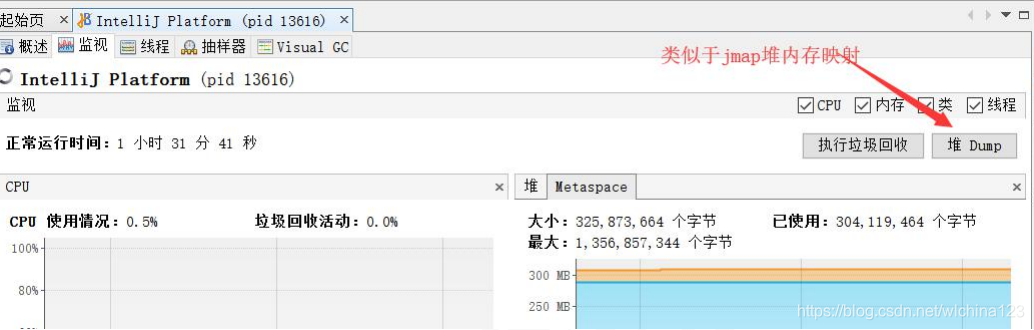

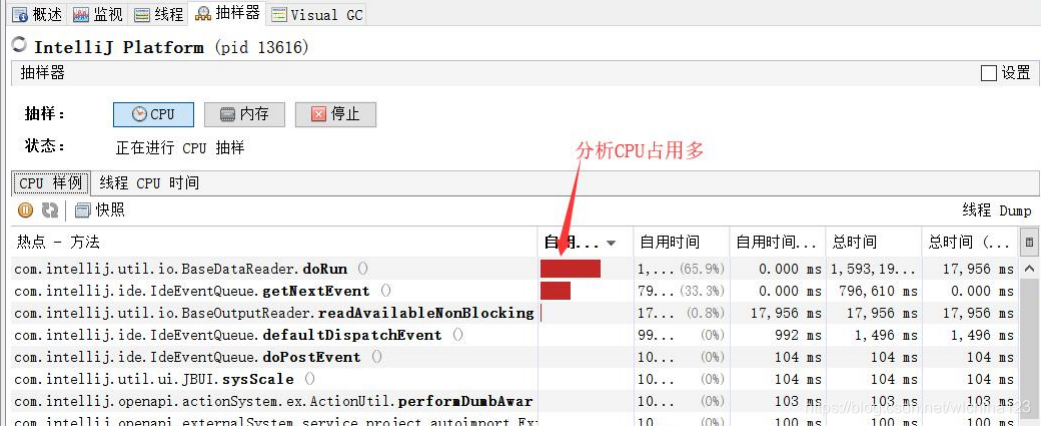
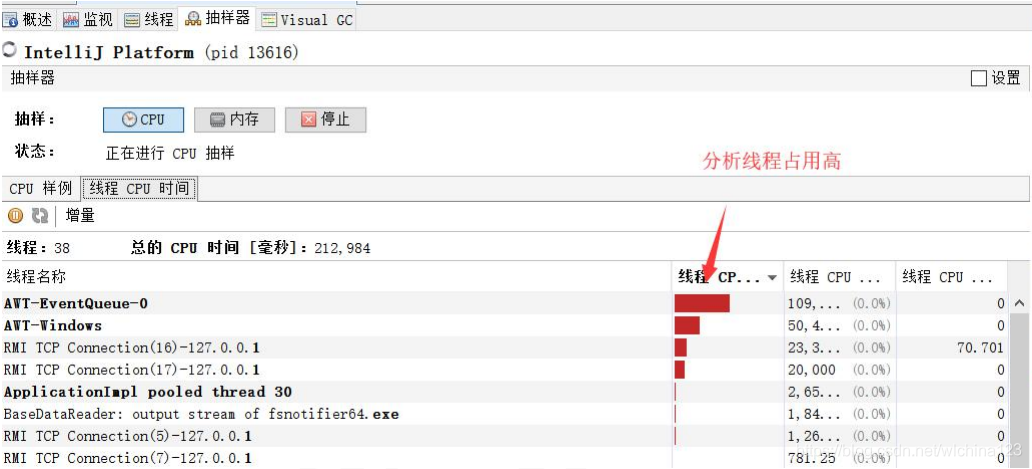
Arthas
https://alibaba.github.io/arthas/
Arthas 是 Alibaba 开源的 Java 诊断工具,支持 JDK 6+,支持 Linux/Mac/Windows,采用命令行交互模式,同时提供丰富的 Tab 自动补全功能,进一步方便进行问题的定位 和诊断下载和安装
不需要安装,就是一个 jar 包 curl -O https://alibaba.github.io/arthas/arthas-boot.jar java -jar arthas-boot.jar 启动 arthas 的 jar 包是 arthas-boot.jar快速入门
1、直接 java -jar arthas-boot.jar。选择 attach 的进程绑定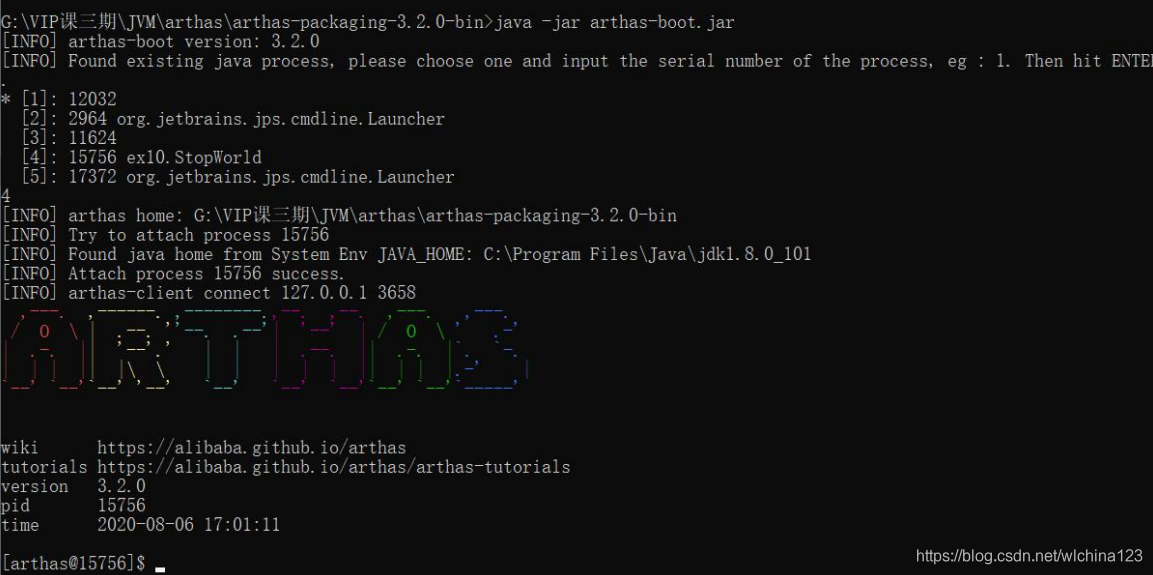 2、通过 jps 命令快速查找 java 进程,再次直接绑定 java -jar arthas-boot.jar pid 启动 arthas 工具 attach 到目标进程
2、通过 jps 命令快速查找 java 进程,再次直接绑定 java -jar arthas-boot.jar pid 启动 arthas 工具 attach 到目标进程 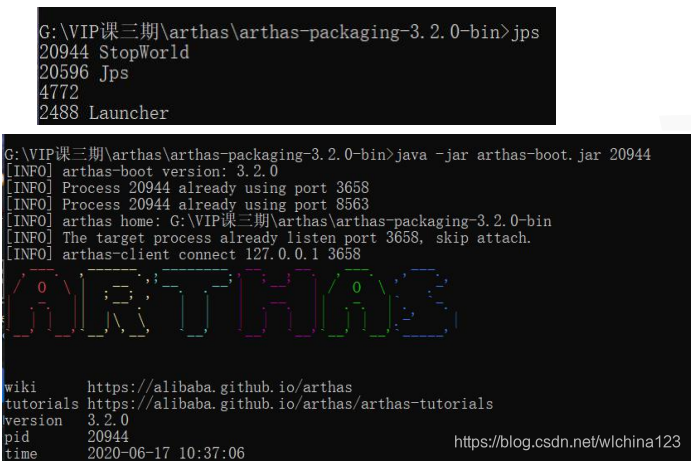 进入 arthas 后命令行前面出现标识
进入 arthas 后命令行前面出现标识  常用命令 Dashboard 注意在 arthas 中,有 tab 键填充功能,所以比较好用。但是这个界面是实时刷新的,一般 5s 刷新一次,使用 q 键退出刷新(没有退出 arthasq)
常用命令 Dashboard 注意在 arthas 中,有 tab 键填充功能,所以比较好用。但是这个界面是实时刷新的,一般 5s 刷新一次,使用 q 键退出刷新(没有退出 arthasq)  Thread 这个命令和 jstack 很相似,但是功能更加强大,主要是查看当前 JVM 的线程堆栈信息 同时可以结合使用 thread –b 来进行死锁的排查死锁 参数解释:
Thread 这个命令和 jstack 很相似,但是功能更加强大,主要是查看当前 JVM 的线程堆栈信息 同时可以结合使用 thread –b 来进行死锁的排查死锁 参数解释: - -n 指定最忙的前 n 个线程并打印堆栈
- -b 找出阻塞当前线程的线程
- -i 指定 cpu 占比统计的采样间隔,单位为毫秒
实战演示:
thread –h 显示帮助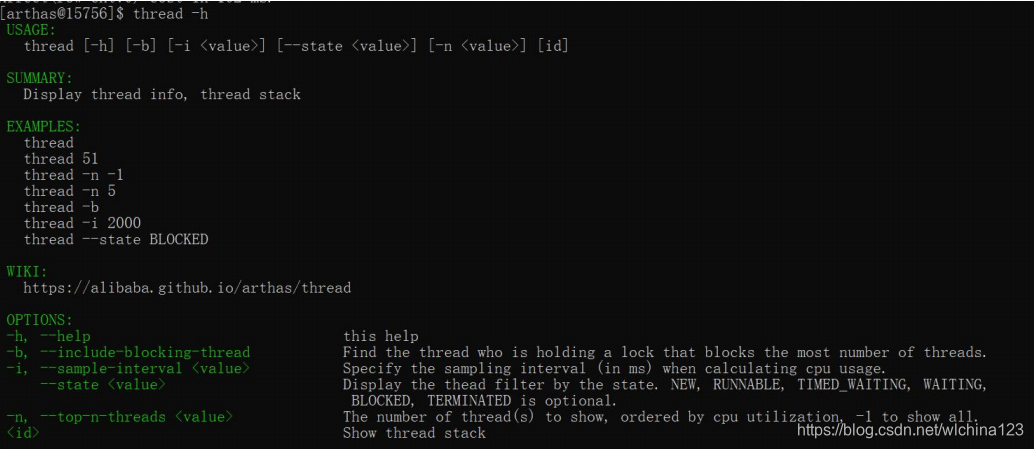 thread –b 找出阻塞当前线程的线程
thread –b 找出阻塞当前线程的线程 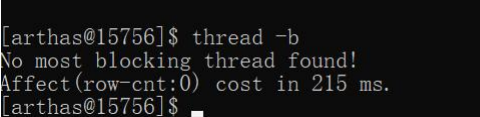 如果有死锁,会有红色的字提醒着,这个阻塞的线程已经被另外一个线程阻塞。
如果有死锁,会有红色的字提醒着,这个阻塞的线程已经被另外一个线程阻塞。  thread -i 1000 -n 3 每过 1000 毫秒进行采样,显示最占 CPU 时间的前 3 个线程
thread -i 1000 -n 3 每过 1000 毫秒进行采样,显示最占 CPU 时间的前 3 个线程 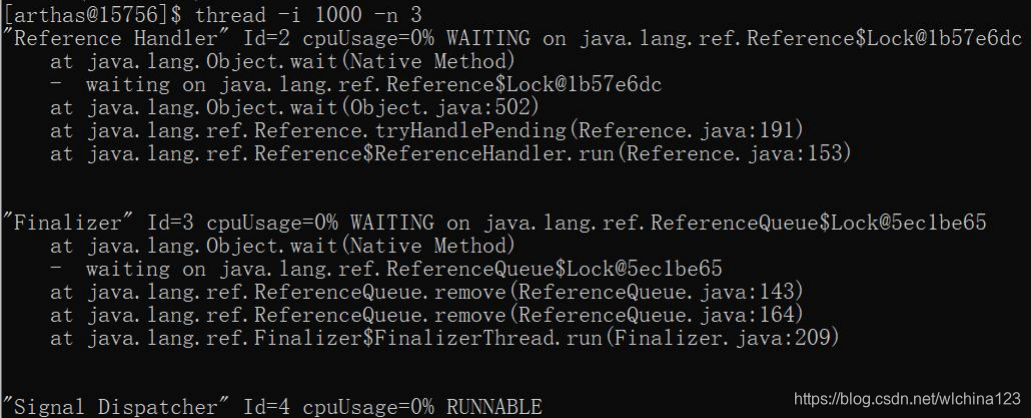 thread --state WAITING 查看处于等待状态的线程
thread --state WAITING 查看处于等待状态的线程  JVM
JVM 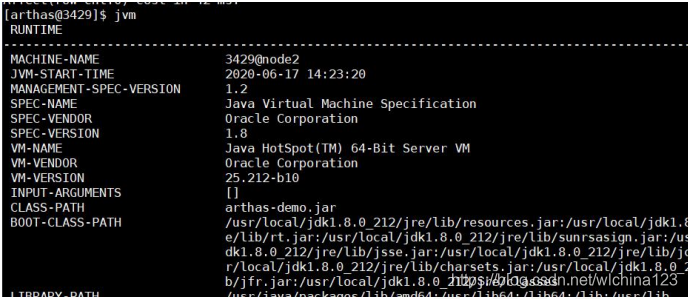 Jad 反编译指定已加载类的源码
Jad 反编译指定已加载类的源码 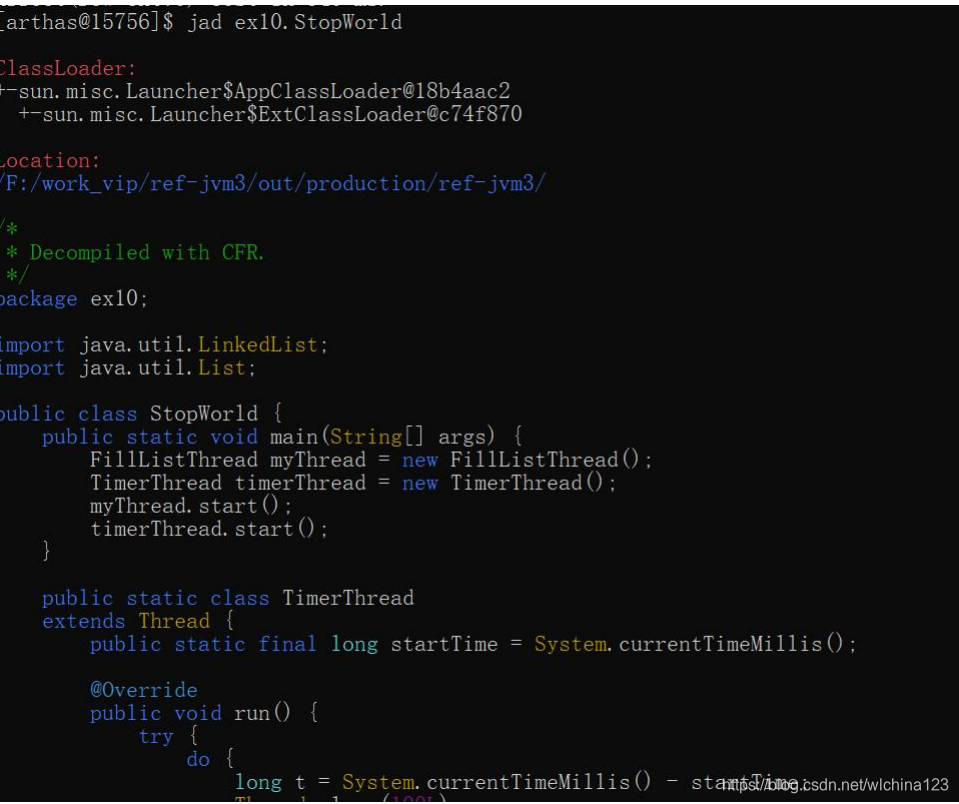 trace 使用 trace 命令可以跟踪统计方法耗时。 继续跟踪耗时高的方法,然后再次访问 比如使用一个 Springboot 项目(当然,不想 Springboot 的话,你也可以直接在 UserController 里 main 方法启动)控制层 getUser 方法调用 了 userService.get(uid);,这个方法中分别进行 check、service、redis、mysql 等操作操作。就可以根据这个命令跟踪出来哪里的耗时最长。
trace 使用 trace 命令可以跟踪统计方法耗时。 继续跟踪耗时高的方法,然后再次访问 比如使用一个 Springboot 项目(当然,不想 Springboot 的话,你也可以直接在 UserController 里 main 方法启动)控制层 getUser 方法调用 了 userService.get(uid);,这个方法中分别进行 check、service、redis、mysql 等操作操作。就可以根据这个命令跟踪出来哪里的耗时最长。  monitor 每 5 秒统计一次 cn.enjoyedu.demo.controller.DemoController 类的 test 方法执行情况
monitor 每 5 秒统计一次 cn.enjoyedu.demo.controller.DemoController 类的 test 方法执行情况  watch watch 观察方法的入参出参信息 # 查看入参和出参 $ watchcn.enjoyedu.demo.controller.DemoController test ‘{params[0],returnObj}’
watch watch 观察方法的入参出参信息 # 查看入参和出参 $ watchcn.enjoyedu.demo.controller.DemoController test ‘{params[0],returnObj}’ 
命令汇总
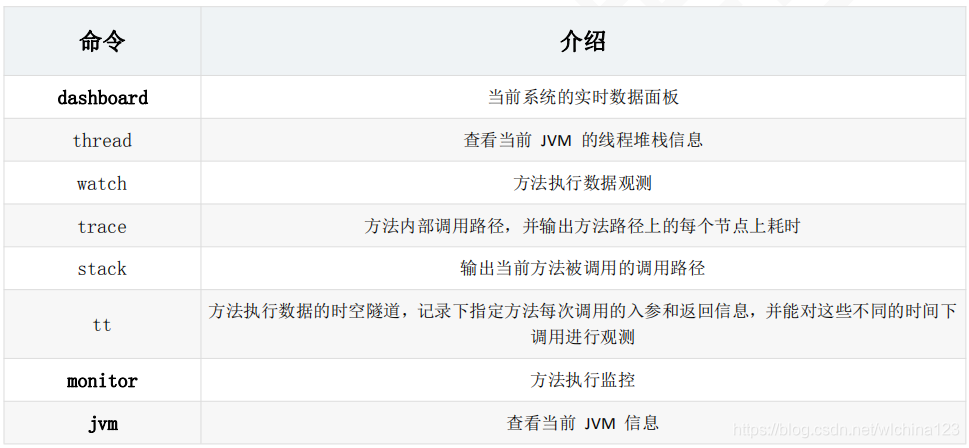
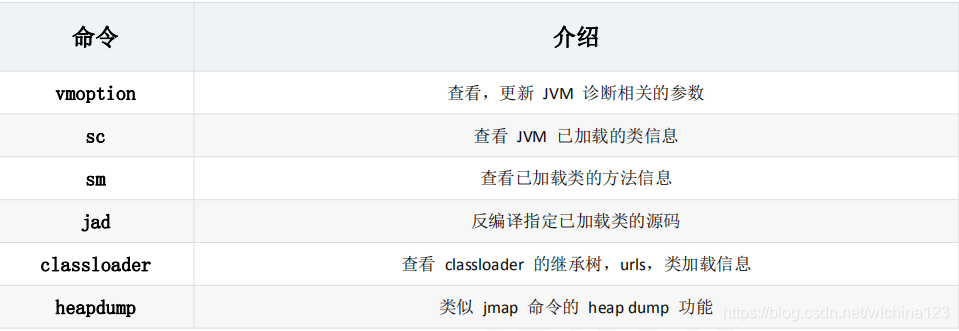
转载地址:http://qhbez.baihongyu.com/
你可能感兴趣的文章
mysql索引能重复吗_mysql “索引”能重复吗?“唯一索引”与“索引”区别是什么?...
查看>>
MySQL索引详解(IT枫斗者)
查看>>
MySQL索引那些事:什么是索引?为什么加索引就查得快了?
查看>>
Mysql索引(1):索引概述
查看>>
Mysql索引(2):索引结构
查看>>
Mysql索引(3):索引分类
查看>>
Mysql索引(4):索引语法
查看>>
mysql级联删除_Mysql笔记系列,DQL基础复习,Mysql的约束与范式
查看>>
mysql练习语句
查看>>
mysql经常使用命令
查看>>
MySQL经常使用技巧
查看>>
mysql给root开启远程访问权限,修改root密码
查看>>
mysql给账号授权相关功能 | 表、视图等
查看>>
MySQL缓存使用率超过80%的解决方法
查看>>
Mysql缓存调优的基本知识(附Demo)
查看>>
mysql编写存储过程
查看>>
mysql网站打开慢问题排查&数据库优化
查看>>
mysql网络部分代码
查看>>
mysql联合索引 where_mysql联合索引与Where子句优化浅析
查看>>
mysql联合索引的最左前缀匹配原则
查看>>